|
THE
GOLDEN RATIO ( Phi )
WHAT IS IT ABOUT ?
Why is Pi (3.14159), for example, so popular and
Phi - not ? How to find it's value? what are the applications of the 'Golden Ratio'?
It was suspected last century that plants use Phi as an optimal solution
to a problem -- but what problem? Only a few years ago
(1993) two French mathematicians Stephan Douady and Yves Couder found a mathematical explanation.It has to do with the way plants grow: From a meristem
(a tiny tip of the growing point of plants) where newcells are formed. The principle nature uses is that of spiral growth
and it produces new cells at a constant rate (or rather a constant amount of turn) for each new "point."
The points may be leaves on a twig, or branches from a trunk, or seeds on a seed head, or petals round the edge. As the
cells are then fixed (and the meristem grows upward and turns again before producing a new "cell") they then grow only outward
and develop.
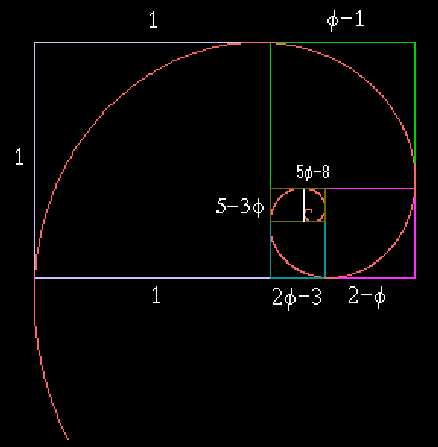
Now, let see the Golden Ratio in
some nonbiotic domain. If we draw a rectangle where one side is equal to some number (whatever number
you like) and the other is equal to that number times the golden ratio, it turns out to be a really pretty rectangle (at least
as pretty as rectangles get). In fact, if I told you to just draw a rectangle on a piece of paper, you'd probably draw one
that came pretty close to the golden ratio. Also, if you then take that rectangle and cut it up into a square and another
rectangle, the rectangle that you make will also have the golden ratio. You can then take the new rectangle and do the same
thing to that, on down forever, and each rectangle you make doing that will have the golden ratio. You can then connect the
corners of these rectangles you've made and it makes a really pretty spiral (called the golden spiral) which has other neat
mathematical properties.
As we learned, a Golden Rectangle is a rectangle in which the ratio of the length to the width is the Golden Ratio.
In other words, if one side of a Golden Rectangle is 2 ft. long, the other side will be approximately equal to 2 * (1.62)
= 3.24.
Now that we know a little about the Golden Ratio and the Golden Rectangle ,let's look a little deeper. Take a line segment
and label its two endpoints A and C. Now put a point B between A and C so that the ratio of the short part of the segment
(BC) to the long part (AB) equals the ratio of the long part (AB) to the entire segment (AC). The ratio of the lengths of
the two parts of this segment is the Golden ratio.
In an equation,we have
AB BC
---- = ---- .
BC AC
Now we're ready for another proof of the Golden ratio. The Golden ratio is the ratio between y and x when
x
y
--- = -----
y x+y
Note that this
is the same as the previous equation, with x substituted for AB and y substituted
for BC.
Let's say x is 1. Then we have
1/y = y/(1+y). If we solve
this equation for y, we'll find that it is (1+sqrt{5})/2,
which is about 1.62.
NOTICE
: If you have a Golden Rectangle and you cut a square off it so that what remains is a rectangle, that remaining rectangle will also be a Golden Rectangle. You can keep cutting these
squares off and getting smaller and smaller Golden Rectangles. (See
the picture above)
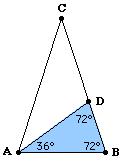
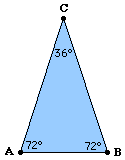
WHAT ABOUT ' GOLDEN TRIANGLE? '
It is an isosceles triangle with vertex angle measuring 36 degrees and base angles measuring 72 degrees. Like the Golden
Rectangle, which has the property that you can cut off a portion of the rectangle that is proportional to the original rectangle,
if you bisect a base angle of the Golden Triangle, you form two new triangles, each similar to the original
triangle. If we assume that the length of each congruent side of the original triangle is 1 and the length of the base is x, each of the congruent
sides of one of the new triangles will be x
and its base will have
length 1 - x.
Setting up the proportion of corresponding sides, we get:
Solving for x we get:
X/(1-X) = 1/X
X = (-1 + sqrt(5)) / 2
Now go back to the original triangle and bisect the vertex. You got two right triangles with acute angles measuring 18
degrees and 72 degrees.
Using the definition of sin A ,
sin A = opposite/hypotenuse and the value of x we just determined
the result
sin 18 = (-1 + sqrt(5)) / 2 = phi/2 = .618/2 = 0.309 ;
PHI is the most irrational number turns out to be a number
already well known in geometry. ( PHI is as well very ubiquitous!)
 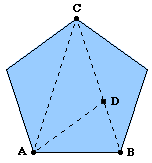
As we can see , PHI = (
V5+ 1)/2 = 1.618033... represents the length of the diagonal in a regular pentagon
of side length 1. This number, known as the "golden
mean," has played a large role in mathematical aesthetics. It is not clear whether its supreme irrationality has anything
to do with its artistic applications. The golden mean can never have a rational approximation as good as 22/7 for Pi , or even as good as 7/5 for 21/2.
|
PHI & HANDWRITING |
|
We all have more knowledge of the Golden Proportion than we ever suspected. Our handwriting shows the Golden
Proportion over and over. When we write, we place a horizontal bar in the capital (upper case) letters, A
E F R B H P quite casually and without any thought. When these letters are enlarged and measured, we see that the
horizontal bar divides the letter into a larger and a smaller part which is usually surprisingly close to the Golden Proportion.
Similarly the horizontal bar of the T is also divided into the Golden Proportion. |
SUMMARIZING
FORMULAE for PHI & phi
PHI - phi = 1 ; PHI/phi =PHI + 1 ;
PHI + phi = V 5 ;
phi /PHI = 1 - phi ;
PHI = 1 + phi ;
PHI = V 5 - phi ;
phi = V
5 - PHI ;
PHI 2 = PHI + 1 ;
phi 2+ phi = 1 ;
PHI(2n+2) = PHI(2n+1)+ PHI2n ;
phi(2n+2) = phi(2n+1)+ phi2n ;
PHI ,phi & Medicine?
|
Not only is our handwriting in
the Golden Proportion but even our hearts beat in the Golden Proportion. |
|
|
|
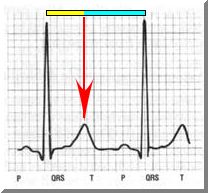
You can see Golden Proportions
between
some elements ECG (electro
cardio gram)
tracings.
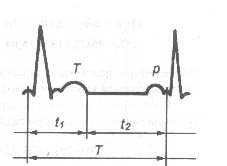
One may select on the cardiogram
two segments of different duration corresponding to systolic (t1) and diastolic (t2) heart activity. There exists the optimal ("golden") palpitation frequency for the
man and for other mammals; the durations of systole, diastole and full cardiac cycle (T) are
in the golden proportion, that is, T : t2 = t2 : t1. So, for example,
for the man this "golden" frequency is equal to 63 heart impacts in one minute, for dogs - 94 that corresponds to actual palpitation
frequency in the rest state.
It's established that
if we take as the measurement unit the middle blood pressure in the aorta then the systolic blood pressure in the aorta is
0.382, and the diastolic pressure is 0.618, that is, their ratio corresponds to the golden proportion. ( 0.618 / 0.382 = 1.618
) It means, that the cardiac performance concerning to the timing cycles and to the blood pressure variation are optimized
by the same principle, the law of the golden proportion.
|

PHI in ARCHITECTURE
|
|
|
The famous Parisian architect, La
Corbusier, wrote a book called "Le Modulor" as a guide to the use of the Golden Proportion in architecture. | We naturally enjoy the golden proportion divisions
of the space of our monuments and homes.


PHI in DESIGN & FASHION All good design abounds with examples of the
Golden Proportion like the clothes or cars. The more skilful the artist the closer his or her art and design conforms
to the Golden Proportion as shown bellow. The dominant landmarks are in the Golden Proportion .



VOILA A 'PHI - TRICK '...
For the Fibonacci sequence show:
Substituting F(n) , F(n+1) , F(n-1) in the formula (1) with (2), (3) , and (4) you can complete
the proof of the trick. Try it and you'll like it !
Another trick?
Pi squared (p2)
and 987
Pi squared (p2) is 9.8696..., which, if you round to 9.87 and ignore the decimals, is 987, the 17th number of the Fibonacci
series !
|

