 |
|
|

FIBONACCI
SERIES
What
does it stand
for ?
LEONARDUS FILIUS BONACCIILeonardo
di Pisa, alias Fibonacci (son of Bonaccio)
lived
in the 12th and 13th century. He is famous for the sequence of numbers that goes by his name. That (infinite)
sequence starts with
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...
The characteristic
of this sequence is that each number is the sum of the previous two.
In other words, if we denote the nth number by Fn, then
Fn+2 = Fn+1 + Fn
The sequence is the solution of a problem which Fibonacci posed
in the year 1202:
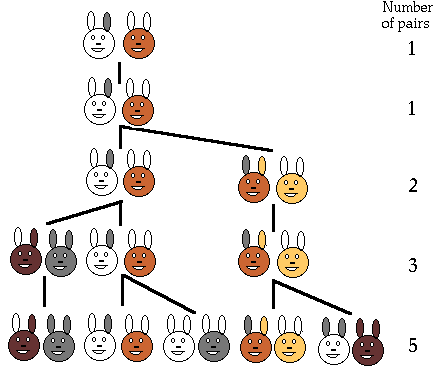
A farmer buys two young rabbits on the marketplace in Pisa: a male
and a female. The first month this couple does not produce little ones, but after the second month the first two rabbits are
born: a male and a female. At the end of each month of the following months this first couple brings into the world two rabbits,
one of each genus. Newborn rabbits start to mate after two months and give birth to a couple of little ones each month.
The
Fibonacci sequence shows how many rabbits the farmer has in the successive months. We suppose that the rabbits never die.
This problem reveals an unrealistic genealogy. A realistic genealogy in which the Fibonacci sequence shows up is the genealogy
of the drones (male bees). A male bee has no father. Fertiliation causes always female bees. So, a male bee has 1 mother and
2 grandparents and 3 great-grandparents (because the male grandparent has no father). Notice the Fibonacci numbers 1,1,2,3,5,...
STOCK MARKET &
SERIES FIBONACCI !
The wave principle of Elliott
The American accountant R.N. Elliott published in 1939 a number of articles in which he explains his theory about
the behaviour of the stock markets. He supposed that the continuous fluctuations in the market are caused by the states of
mind of the mass, which are wavered between pessimism and optimism.
In figure
1 we see an elementary undulation. First the price rises fast and then relapses. During a longer period of time we recognize
a pattern like (stylistically) shown in the second figure. We see three ascending and two descending intervals on the left
side of the apex and 2 descending intervals and 1 ascending interval on the right side of the apex. After intensive study
over a longer period of time about the behaviour of the stock market of Wall Street, Elliott found out that in every exchange
diagram this characteristic pattern existing of 5 intervals left from the top and 3 right from the top is repeated contiguously
and on each scale. Let's take a closer look at this phenomenon.
If we project figure 1 and 2 on each other we see that
the top and the edges coincide. You can regard figure 2 as a refinement of figure 1 caused by measuring over a longer period
of time. (Note that this is a stylistic picture of the reality; the form can vary, and there may be 20 peaks, but the pattern
of 5 intervals left and 3 right from the top is always there.) Figure 3 is a stock market graph over a still longer period
of time. We see that this graph is a refinement of figure 2. We may continue this process over an unlimited period of time.
Let us put the number of
intervals in a table.
|
figure |
Right |
Left |
Together |
|
figure 1 |
1
|
1
|
2
|
|
figure 2 |
3
|
5
|
8
|
|
figure 3 |
13
|
21
|
34
|
We recognize the
sequence of Fibonacci.
Let's find an explanation for that. Note that there are two kinds of intervals. The first kind (A)
will be divided into 3 parts and the other (B) into 5 parts. We split up the previous table:
|
figure |
Right (A) |
Right (B) |
Left (A) |
Left (B) |
|
figure 1 |
1
|
0
|
0
|
1
|
|
figure 2 |
1
|
2
|
2
|
3
|
|
figure 3 |
5
|
8
|
8
|
13
|

|
 |
|
WHERE
WE CAN SEE FIBONACCI
NUMBERS ?
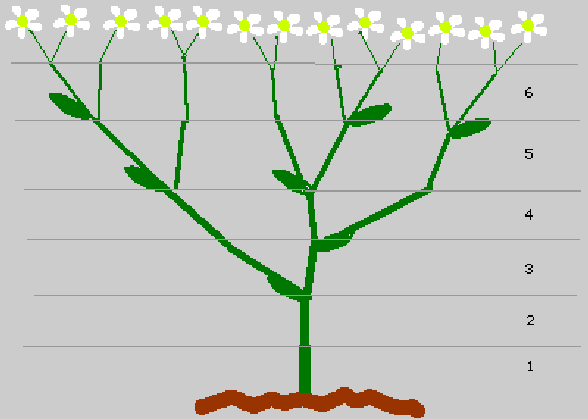
Branching plantsSome plants show the Fibonacci numbers in the number
of "growing points". Suppose that when a plant puts out a new shoot, that shoot
has to grow two months before it is strong enough to support branching. If it branches every month after that at the growing
point, we get the picture shown here.

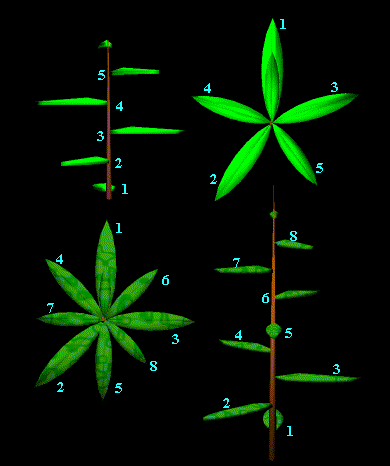
Leaf arrangements
The Fibonacci numbers occur when counting both the number of
times we go around the stem, going from leaf to leaf, as well as counting the leaves we meet until we encounter a leaf directly
above the starting one. If we count in the other direction, we get a different number of turns for the same number of leaves.
The number of turns in each direction and the number of leaves met are three consecutive Fibonacci numbers!
For example, in the top plant in the picture , we have 3 clockwise rotations before we meet a leaf directly
above the first, passing 5 leaves on the way. If we go anti-clockwise, we need only 2 turns.
Notice that 2, 3 and 5 are consecutive Fibonacci numbers.For the lower plant in the picture, we have 5 clockwise
rotations passing 8 leaves, or just 3 rotations in the anti-clockwise direction. This time
3, 5 and 8 are consecutive numbers in the Fibonacci sequence.We can write this as, for the top plant, 3/5 clockwise
rotations per leaf ( or 2/5 for the anticlockwise direction).
90 percent of all plants exhibit this pattern
of leaves involving the Fibonacci numbers. For example : 1/2 - elm, linden, lime, grasses; 1/3 - beech,
hazel, grasses, blackberry ; 2/5 - oak, cherry, apple, holly, plum, common groundsel;
3/8 - poplar, rose, pear, willow ; 5/13 pussy willow, almond.

Petals on flowers
On many plants, the number of petals is a Fibonacci number:
buttercups
have 5 petals; lilies and iris have 3 petals; some delphiniums have 8; corn marigolds have 13 petals; some asters have 21
whereas daisies can be found with 34, 55 or even 89 petals. Tthe orange "petals" seem to form spirals
curving both to the left and to the right. At the edge of the picture, if you count those spiralling to the right as you go
outwards, there are 55 spirals. A little further towards the centre and you can count 34 spirals. You will see that the pair
of numbers (counting spirals in curving left and curving right) are neighbours in the Fibonacci series.

FLOWER SEEDS
Fibonacci numbers can also be seen in the arrangement of
seeds on
flower heads.
Take a look !
Each section of your index finger,
from the tip to the base of the wrist, is larger than the preceding one by about the Fibonacci ratio of 1.618, also fitting
the Fibonacci numbers 2, 3, 5 and 8.
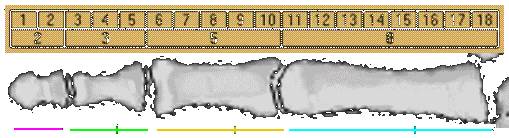
By this scale, your finger nail is 1 unit in length. Curiously enough , we have also 2 hands , each with 5 digits, and our 8 fingers are
each comprised of 3 sections .
All Fibonacci numbers !

Phibonacci numbers in the
SOLAR GEOMETRY ?
Venus orbits the Sun in 224.695 days while Earth orbits the Sun in 365.242 days creating
a ratio of 8/13 ( both Fibonacci numbers ), or o.615 ( roughly phi). Thus, 5 conjunctions of Earth and Venus occur every
8 orbits of the Earth around the Sun and every 13 orbits of Venus .
|
 |
|
|
 |
|
|
 |
|
|
 |
 |
|
Here is a little trick...
Voila a trick you can perform
on friends which seems to show that you have amazing mathematical powers.
Choose, any
two numbers you like, dear reader, but not too big as you're going to have to do some adding yourself. Write them as if you
are going to add them up and I'll, of course, be looking the other way!
. Suppose you choose 16 and
21 .
Now add the first to the second and write
the sum underneath to make the third entry in the column.
So, you got :
|
(16+21) under the other two: |
16 |
|
21 |
|
37 |
Add up the second and your new number and again
write their sum underneath. Keep on doing this, adding the number you have just written to the number before it and putting
the new sum underneath. Stop when you have 10 numbers written down and draw a line under the tenth.
.
|
Your column now looks like this: |
16
21
37
58
95
153
248
401
649
1050
|
Now I'll turn round and look at your numbers
and write the sum of all ten numbers straight away -- 2728
.
You make the sum on your calculator and feel amazed
that I got it right in so short a time [gasp!]
So how did I do it?
The sum of all ten numbers is just
eleven times the fourth number from the bottom. Also, I use the quick method of multiplying
a number by eleven. The fourth number from the bottom is 248, and there is the quick and easy method of multiplying numbers
by 11 that you can easily do in your head:
|
Starting at the right, just copy the last digit of the number as the last digit
of your product. Here the last digit of 248 is 8 so the product also ends with 8 which I write down: |
...
248
401
649
1050
8 |
|
Now, continuing in 248, keep adding up from the right each number and its neighbour,
in pairs, writing down their sum as you go. If ever you get a sum bigger than 10, then write down the units digit of the sum
and remember to carry anything over into your next pair to add.
Here the pairs of 248 are (from the right) 4+8 and then
2+4. So, next to the 8 I have "4+8=12" so I write 2 and remembers there is an extra one to add on to the next pair: |
...
248
401
649
1050
28 |
|
Then 2+4 is 6, adding the one carried makes 7, so she writes 7 on the left of those digits already written down: |
...
248
401
649
1050
728 |
|
Finally copy down the left hand digit (plus any carry); the left digit is 2
which, because there is nothing being carried from the previous pair, becomes the left-hand digit of the sum.
The final sum is therefore 2728 = 11 x 248 . |
...
248
401
649
1050
2728 |
Why does it work?
You can see how it works using algebra and by starting with A and B as the
two numbers you choose.
What we write next? Just A+B in algebraic form.
The next sum is B added to
A+B which is A+2B.
The other numbers in the column are 2A+3B, 3A+5B, ... up to 21A+34B. A B A + B A + 2B 2A + 3B 3A + 5B 5A + 8B 8A +13B 13A +21B 21A +34B -------- 55A +88B
If you add these up you find the total sum of all ten is 55A+88B.
Now look
at the fourth number up from the bottom. What is it?
How is it related to the final sum of 55A+88B?
Hint : 11(5A + 8B) = 55A + 88B
So the trick works by a special property
of adding up exactly ten numbers from a Fibonacci-like sequence and will work for any two starting values A and B!
Perhaps you noticed that the
multiples of A and B were the Fibonacci numbers? Isn't there a connection with the notice of Mesoamericans, who recognized the numbers
7 and 11 as special?
Some interesting properties
Fibonacci
numbers have many fascinating properties:
1. The sum of Fibonacci numbers at any given
point in the sequence is never a Fibonacci number itself, but
if you add the second number in the sequence to this sum, the result is the number two terms ahead.
For example, in the sequence 1, 1, 2, 3, 5, 8, (13), 21, add the first six numbers, skip the seventh, and you
get the eighth minus the second number, one.
2. Take any three numbers in the sequence (like 3, 5,
8); square the middle number (5 x 5 = 25); multiply the first and third numbers (3 x 8 = 24); the difference between the
two answers is always one.
3.Take any four numbers in the sequence, in order,
multiply the two outside numbers and then multiply the two inside numbers. The first product will be either one
more or one less than the second:
2, 3, 5, 8
3, 5, 8, 13
2 x 8 = 16; 3 x 5 = 15
3 x 13 = 39; 5 x 8 = 40
|
|
